- PH. CL´EMENT, P. Felmer and E. MITIDIERI, Homoclinic orbits for a class of infinite dimensional Hamiltonian systems, Annali de la Scuola Normale Superiore de Pisa. Serie IV. Vol. XXIV. Fasc. 2, 1997, 367-393.
- C. Cortázar, M. Elgueta and P. Felmer, Existence of signed solutions for a semilinear elliptic boundary value problem. Diff. Int. Equat., 7 (1)(1994), 293-299.
-
C. Cortázar, M. Elgueta and P. Felmer, On a semilinear elliptic
problem in
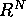 with a non-Lipschitzian non-linearity, Adv. in Diff. Eq., Vol. 1,
No. 2, (1996), 199-218.
with a non-Lipschitzian non-linearity, Adv. in Diff. Eq., Vol. 1,
No. 2, (1996), 199-218. - C. Cortázar, M. Elgueta and P. Felmer, Symmetry in an elliptic problem and the blow-up set of a quasilinear heat equation, Comm. in P.D.E., 21 (1996), 507-520.
-
C. Cortázar, M. Elgueta and P. Felmer, Uniqueness
of positive solutions of
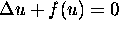 in
in 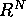 ,
,  , Arch. Rational Mech. Anal. 142 (1998), 127-141.
, Arch. Rational Mech. Anal. 142 (1998), 127-141. -
C. Cortázar, M. Elgueta and P. Felmer, Some uniqueness
results for
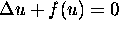 in
in 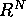 ,
,  , Reaction diffusion systems. Lecture Notes Pure Appl Math 194, Marcel
Dekker, (1998).
, Reaction diffusion systems. Lecture Notes Pure Appl Math 194, Marcel
Dekker, (1998). - A. AVILA and P. Felmer, Periodic and subharmonic solutions for a class of second order Hamiltonian systems, Dynamic Systems and Applications, Vol. 3, No 4, (1994), 519-536.
- D. DE FIGUEIREDO and P. Felmer, On superquadratic elliptic systems, Trans. AMS, Vol. 343, No 1, (1994), 99-116.
- PH. CL´EMENT, P. Felmer and E. MITIDIERI, Solutions homoclines d'un systeme hamiltonien non-borné et superquadratique, C.R. Acad. Sci. Paris, t. 320, Série I, (1995), 1481-1484.
- M. del Pino and P. Felmer, Multiple solutions for a semilinear elliptic equation, Trans. AMS, vol. 347, N. 12, 1995.
- M. del Pino and P. Felmer, Locally Energy-Minimizing Solutions of the Ginzburg Landau Energy, C.R. Acad. Sci. Paris, t. 321, Série I, (1995), 1207-1211.
- M. del Pino and P. Felmer, Least energy solutions to semilinear elliptic equations in unbounded domains, Proc. Roy. Soc. Edinburgh, 126A (1996), 195-208.
- M. del Pino and P. Felmer, Local mountain passes for semilinear elliptic problems in unbounded domains, Calc. of Variations and PDE's 4 (1996), 121-137.
- M. del Pino and P. Felmer, Bound states of nonlinear Schrödinger equations, J. of Functional Analysis149 (1997), 245-265.
- M. del Pino and P. Felmer, Localizing spike-layer patterns in singularly perturbed elliptic problems, Proceedings Asymptotics in nonlinear diffusive systems Math. Inst. Tohoku University, Sendai, Japan July 28-August 1, 1997. Tohoku Mathematical Publications 8 (1998).
- M. del Pino and P. Felmer, Multi-peak bound states of nonlinear Schrödinger equations, Ann. Inst. H. Poincaré Analyse Nonlineaire 15 (1998), 127-149.
- M. del Pino and P. Felmer, Local minimizers of the Ginzburg-Landau Energy, Math. Zeitschrift 225 (1997), 671-684.
- M. del Pino, P. Felmer and O. MIYAGAKI, Existence of Positive Bound States of Nonlinear Schrödinger Equations with Saddle-like Potential, Nonlinear Analysis Vol 34, No 7, 1998, 979-989.
- M. del Pino and P. Felmer, On the basic concentration estimate for the Ginzburg-Landau energy, Diferential and Integral Equations11, No 5, 1998, 771-779.
- M. del Pino, P. Felmer and J. WEI, On the role of distance function on certain elliptic singular perturbation problems, to appear in Comm. in Partial Diff. Equations.
- M. del Pino, P. Felmer and J. WEI, On the role of curvature on certain elliptic singular perturbation problems, to appear in SIAM J. Math. Anal.
- M. del Pino, P. Felmer and J. WEI, Multi-peak Solutions For Some Singular Perturbation Problems', to appear in Calc. of Variations and PDE's.
- M. del Pino and P. FELMER, Spike-layered solutions of singularly perturbed elliptic problems in a degenerate setting, to appear in Indiana University Mathematical Journal.
- P. Felmer and R. Manásevich, Periodic solutions of a coupled system of telegraph-wave equations, J. Math. Anal. Appl. Vol. 116, No. 1, (1986), 10-21.
-
P. Felmer, Multiple solutions of Lagrangean systems in
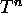 , Nonlinear Analysis TMA, Vol. 15, No. (1990), 815-831.
, Nonlinear Analysis TMA, Vol. 15, No. (1990), 815-831. - P. Felmer, Subharmonics near an equilibrium point for Hamiltonian Systems, Manuscripta Mathematica 66 1990, 359-396.
- P. Felmer, Heteroclinic orbits for spatially periodic Hamiltonian systems, Analyse Nonlineaire A.I.H.P., Vol. 8, No. 5 (1991), 477-497.
- P. Felmer, R. Manásevich and F. DE THELIN, Existence and uniqueness of positive solutions for certain quasilinear elliptic systems, Comm. in P.D.E., Vol. 17, No. 11& 12, (1992), 2013-2029.
- P. Felmer, Rotation type solutions for superquadratic Hamiltonian systems, Nonlinear Analysis TMA, Vol. 19, No.5, (1992), 409-425.
- P. Felmer, Periodic solutions of spatially periodic Hamiltonian Systems, Journal of Differential Equations, Vol. 98, No. 1, (1992).
- P. Felmer and E. SILVA, Subharmonics near an equilibrium for some second order hamiltonian systems, Proceedings of the Royal Society of Edinburgh, 123A (1993), 819-834.
- P. Felmer, Periodic Solutions of `superquadratic' Hamiltonian systems B, Journal of Differential Equations, Vol. 102, No. 1, (1993), 188-207.
- P. Felmer and R. Manásevich, A global approach for bifurcation from a non-degenerate periodic solution, Nonlinear Analysis TMA, Vol. 22, No 3, (1994), 353-361.
-
P. Felmer, Nonexistence and symmetry theorems for elliptic
systems in
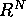 ,
Rendiconti del Circolo Matematico de Palermo, Serie II-Tomo XLIII,
(1994), 259-284.
,
Rendiconti del Circolo Matematico de Palermo, Serie II-Tomo XLIII,
(1994), 259-284. -
P. Felmer and S. MARTf
INEZ, Existence and Uniqueness of positive solutions for certain differential systems, Advances in Differential Equations 3 No 4, 1998, 575-593. - P. Felmer and E. SILVA, Homoclinic and periodic orbits for Hamiltonian Systems, to appear in Annali de la Scuola Normale Superiore de Pisa.
- P. Felmer and K. TANAKA, Hyperbolic-like solutions for singular Hamiltonian Systems, to appear in Nonlinear Differential Equations and Applications.
- P. Felmer and X. Q. WANG, Multiplicity for Symmetric indefinite functionals: Applications to Hamiltonian and Elliptic Systems, to appear in Topological Methods in Nonlinear Analysis.
D. DE FIGUEIREDO and P. Felmer, A Liouville-type theorem for elliptic systems, Annali de la Scuola Normale Superiore de Pisa, Serie IV. Vol. XXI. Fasc. 3, (1994), 387-397.