- La Universidad

-
Facultades
- Agronomía e Ingeniería Forestal
- Arquitectura, Diseño y Estudios Urbanos
- Artes
- Ciencias Biológicas
- Ciencias Económicas y Administrativas
- Ciencias Sociales
- Comunicaciones
- Derecho
- Educación
- Filosofía
- Física
- Historia, Geografía y Ciencia Política
- Ingeniería
- Letras
- Matemáticas
- Medicina
- Química
- Teología
- College
- Campus Villarrica

- Organizaciones Vinculadas

- Bibliotecas

- Mi Portal UC

- Correo UC
Quédate en casa: Chile necesita reducir la tasa de crecimiento del COVID-19 al menos al 7%

2020-04-13
- ¿Cuáles son las posibilidades de vencer al COVID-19? ¿Son suficientes las medidas tomadas? Las matemáticas nos ayudan a resolver estas interrogantes.
Estamos viviendo una pandemia a nivel mundial y aunque lamentamos el fallecimiento de decenas de compatriotas, hemos tenido buenas noticias como país, debido al descenso en la tasa de crecimiento local del virus.
“¿Podemos cantar victoria? No; ¿podemos vencer la pandemia? Sí”, son las esperanzadoras reflexiones de los académicos de la Facultad de Matemáticas de la UC y doctores en Matemática, Duván Henao y Gregorio Moreno.
De acuerdo con las predicciones basadas en el Sistema SIR* (ver imagen), con información hasta el 12 de abril de 2020, “si seguimos así, se espera que los hospitales de Chile colapsen en junio”, explican.
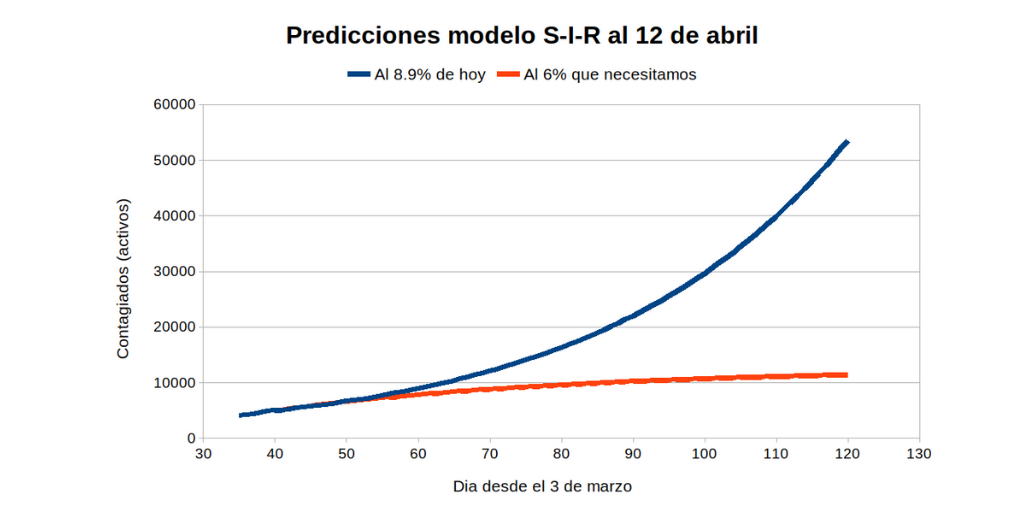
“En España e Italia ya están frenando el virus: ¿Cómo podemos hacerlo nosotros? En ambos países europeos, la tasa de crecimiento (nuevos casos dividido por infectados activos) bajó al 6% y al 4.1%, respectivamente; en Chile sigue en 8.9%. Aunque este porcentaje es mejor que el 20% que se registraba a fines de marzo (el aislamiento empieza a dar frutos), no superaremos la pandemia si no bajamos al 7% (idealmente, al 6%)”, explica el profesor Moreno.
“La última semana se recuperaron más de 1400 personas, pero hubo más de 2700 casos nuevos. Necesitamos que esto se invierta, o sea, que haya más recuperados que nuevos infectados. Es por eso que el llamado a que las personas que pueden mantener aislamiento voluntario y aquellas que se encuentran en zonas de cuarentena, se queden en casa ¡Lleguemos a la meta! Juntos podemos reducir la tasa de crecimiento del virus al menos a un 7%”, indica el profesor Henao.
Si no tienes la obligación de salir, si puedes hacer cuarentena voluntaria, #QuédateEnCasa, es el llamado.
Sobre el modelo SIR
Una descripción concisa pero rigurosa del sistema SIR, se puede encontrar en el artículo “Evolución de las epidemias: La Matemática de aislarse”, de los investigadores Héctor Pastén (Facultad de Matemáticas UC) y Jorge Castillo (Z Data Lab):
"El llamado modelo SIR, es un modelo matemático desarrollado en 1927 y que hasta el día de hoy es la base para otros modelos más sofisticados en el estudio de epidemias. SIR toma en cuenta aspectos de la propagación de una epidemia, que el modelo exponencial no considera: que después de un cierto tiempo, los enfermos se recuperan (o lamentablemente, fallecen) y dejan de ser contagiosos (al menos por un tiempo); que mientras más infectados hay, menos personas sanas quedan susceptibles de ser contagiadas.
La sigla viene de catalogar los miembros de una comunidad (digamos, un país) en tres tipos:
“¿Podemos cantar victoria? No; ¿podemos vencer la pandemia? Sí”, son las esperanzadoras reflexiones de los académicos de la Facultad de Matemáticas de la UC y doctores en Matemática, Duván Henao y Gregorio Moreno.
De acuerdo con las predicciones basadas en el Sistema SIR* (ver imagen), con información hasta el 12 de abril de 2020, “si seguimos así, se espera que los hospitales de Chile colapsen en junio”, explican.

“En España e Italia ya están frenando el virus: ¿Cómo podemos hacerlo nosotros? En ambos países europeos, la tasa de crecimiento (nuevos casos dividido por infectados activos) bajó al 6% y al 4.1%, respectivamente; en Chile sigue en 8.9%. Aunque este porcentaje es mejor que el 20% que se registraba a fines de marzo (el aislamiento empieza a dar frutos), no superaremos la pandemia si no bajamos al 7% (idealmente, al 6%)”, explica el profesor Moreno.
“La última semana se recuperaron más de 1400 personas, pero hubo más de 2700 casos nuevos. Necesitamos que esto se invierta, o sea, que haya más recuperados que nuevos infectados. Es por eso que el llamado a que las personas que pueden mantener aislamiento voluntario y aquellas que se encuentran en zonas de cuarentena, se queden en casa ¡Lleguemos a la meta! Juntos podemos reducir la tasa de crecimiento del virus al menos a un 7%”, indica el profesor Henao.
Si no tienes la obligación de salir, si puedes hacer cuarentena voluntaria, #QuédateEnCasa, es el llamado.
Sobre el modelo SIR
Una descripción concisa pero rigurosa del sistema SIR, se puede encontrar en el artículo “Evolución de las epidemias: La Matemática de aislarse”, de los investigadores Héctor Pastén (Facultad de Matemáticas UC) y Jorge Castillo (Z Data Lab):
"El llamado modelo SIR, es un modelo matemático desarrollado en 1927 y que hasta el día de hoy es la base para otros modelos más sofisticados en el estudio de epidemias. SIR toma en cuenta aspectos de la propagación de una epidemia, que el modelo exponencial no considera: que después de un cierto tiempo, los enfermos se recuperan (o lamentablemente, fallecen) y dejan de ser contagiosos (al menos por un tiempo); que mientras más infectados hay, menos personas sanas quedan susceptibles de ser contagiadas.
La sigla viene de catalogar los miembros de una comunidad (digamos, un país) en tres tipos:
-Susceptibles: Personas sanas que no son inmunes. Es decir, son susceptibles a ser infectadas.
-Infectados: Personas portadoras de la enfermedad y que pueden contagiar a otros
-Retirados: Personas que estuvieron enfermas y que se recuperaron (o que lamentablemente fallecieron) y, por ende, dejan de ser contagiosas.
El modelo SIR, en su forma más sencilla, es un sistema de tres ecuaciones diferenciales relacionando la cantidad de personas en estos tres grupos y cómo varían a través del tiempo”.
*Las proyecciones aquí presentadas están detalladas en el artículo “Evolución de las epidemias: La Matemática de aislarse”, de los investigadores Héctor Pastén (Facultad de Matemáticas UC) y Jorge Castillo (Z Data Lab) y en "Coronavirus: desde las ecuaciones de un desastre a una matemática de la esperanza" del investigador Gregorio Moreno (Facultad de Matemáticas UC)
CORONAVIRUS: DESDE LAS ECUACIONES DE UN DESASTRE A UNA MATEMÁTICA DE LA ESPERANZA
El modelo SIR, en su forma más sencilla, es un sistema de tres ecuaciones diferenciales relacionando la cantidad de personas en estos tres grupos y cómo varían a través del tiempo”.
*Las proyecciones aquí presentadas están detalladas en el artículo “Evolución de las epidemias: La Matemática de aislarse”, de los investigadores Héctor Pastén (Facultad de Matemáticas UC) y Jorge Castillo (Z Data Lab) y en "Coronavirus: desde las ecuaciones de un desastre a una matemática de la esperanza" del investigador Gregorio Moreno (Facultad de Matemáticas UC)
CORONAVIRUS: DESDE LAS ECUACIONES DE UN DESASTRE A UNA MATEMÁTICA DE LA ESPERANZA





