Seminario de Análisis y Geometría
Los seminarios de Análisis y Geometría se llevan a cabo los días jueves a las 16:10 en la Sala 2 de la Facultad de Matemáticas, Pontificia Universidad Católica de Chile.Organizadores: Pedro Gaspar y Gianmarco Sperone
2022-05-31
16:00hrs.
16:00hrs.
Cesar Arias. PUC
Geometría y Holografía
Sala 2, edificio Rolando Chuaqui
Abstract:
Revisaremos las diferentes texturas geométricas que aparecen en la formulación más simple (en el límite de baja energía) de la correspondencia AdS/CFT. En particular, mostraremos como técnicas en geometría conforme pueden ser usadas para el cálculo de anomalías e invariantes conformes. Finalmente propondremos una extensión de las ideas anteriores, la cual surge naturalmente al tratar defectos como bordes generalizados.
Geometría y Holografía
Sala 2, edificio Rolando Chuaqui
Abstract:
Revisaremos las diferentes texturas geométricas que aparecen en la formulación más simple (en el límite de baja energía) de la correspondencia AdS/CFT. En particular, mostraremos como técnicas en geometría conforme pueden ser usadas para el cálculo de anomalías e invariantes conformes. Finalmente propondremos una extensión de las ideas anteriores, la cual surge naturalmente al tratar defectos como bordes generalizados.
2022-05-10
16:00hrs.
16:00hrs.
Gabrielle Nornberg . Departamento de Ingeniería Matemática, Universidad de Chile
Propiedades cualitativas para sistemas de tipo Lane-Emden
Sala 2, edificio Rolando Chuaqui
Abstract:
En esta charla discutiremos algunas propiedades cualitativas de soluciones de sistemas de tipo Lane-Emden y sus aplicaciones a la existencia y no existencia de soluciones.
Propiedades cualitativas para sistemas de tipo Lane-Emden
Sala 2, edificio Rolando Chuaqui
Abstract:
En esta charla discutiremos algunas propiedades cualitativas de soluciones de sistemas de tipo Lane-Emden y sus aplicaciones a la existencia y no existencia de soluciones.
2022-04-19
16:00hrs.
16:00hrs.
Diego Navarro. Impa, Brasil
Genuine deformations of Euclidean hypersurfaces in higher codimensions
Sala 2, edificio Rolando Chuaqui
Abstract:
Sbrana and Cartan gave local classifications for the set of Euclidean hypersurfaces $M^n\subseteq\mathbb{R}^{n+1}$ which admit another non-congruent isometric immersions in $\mathbb{R}^{n+1}$ for $n\geq 3$. Such isometric immersion is called a genuine deformation of the hypersurface. The main goal of this paper is to extend their classification to higher codimensions. The main result of this presentation is to describe the genuine deformations of some hypersurfaces in arbitrary codimension. As a consequence, we obtain an analogous classification to the one given by Sbrana and Cartan giving all local isometric immersions in $\mathbb{R}^{n+2}$ of a generic hypersurface $M^n\subseteq\mathbb{R}^{n+1}$ for $n\geq 4$. In addition, the techniques developed here can be used to study conformally flat Euclidean submanifolds.
Genuine deformations of Euclidean hypersurfaces in higher codimensions
Sala 2, edificio Rolando Chuaqui
Abstract:
Sbrana and Cartan gave local classifications for the set of Euclidean hypersurfaces $M^n\subseteq\mathbb{R}^{n+1}$ which admit another non-congruent isometric immersions in $\mathbb{R}^{n+1}$ for $n\geq 3$. Such isometric immersion is called a genuine deformation of the hypersurface. The main goal of this paper is to extend their classification to higher codimensions. The main result of this presentation is to describe the genuine deformations of some hypersurfaces in arbitrary codimension. As a consequence, we obtain an analogous classification to the one given by Sbrana and Cartan giving all local isometric immersions in $\mathbb{R}^{n+2}$ of a generic hypersurface $M^n\subseteq\mathbb{R}^{n+1}$ for $n\geq 4$. In addition, the techniques developed here can be used to study conformally flat Euclidean submanifolds.
2022-03-22
16:00hrs.
16:00hrs.
Tobias Ried. Lmu Munich & Mpmi Leipzig
A variational approach to the regularity of optimal transportation
Sala 2, edificio Rolando Chuaqui
Abstract:
In this talk I want to present a purely variational approach to the regularity theory for the Monge-Ampère equation, or rather optimal transportation, introduced by Goldman—Otto. Following De Giorgi’s strategy for the regularity theory of minimal surfaces, it is based on the approximation of the displacement by a harmonic gradient, which leads to a one-step improvement lemma, and feeds into a Campanato iteration on the C^{1,\alpha}-level for the displacement. We extend the result of Goldman—Otto for the Euclidean cost function to the case of general cost functions. One of the new contributions is the use of almost-minimality: if the cost is quantitatively close to the Euclidean cost function, a minimiser for the optimal transport problem with general cost is an almost-minimiser for the one with quadratic cost. This allows us to reprove the C^{1,\alpha}-regularity result of De Philippis—Figalli, bypassing Caffarelli’s celebrated theory. (This is joint work with F. Otto and M. Prod’homme)
A variational approach to the regularity of optimal transportation
Sala 2, edificio Rolando Chuaqui
Abstract:
In this talk I want to present a purely variational approach to the regularity theory for the Monge-Ampère equation, or rather optimal transportation, introduced by Goldman—Otto. Following De Giorgi’s strategy for the regularity theory of minimal surfaces, it is based on the approximation of the displacement by a harmonic gradient, which leads to a one-step improvement lemma, and feeds into a Campanato iteration on the C^{1,\alpha}-level for the displacement. We extend the result of Goldman—Otto for the Euclidean cost function to the case of general cost functions. One of the new contributions is the use of almost-minimality: if the cost is quantitatively close to the Euclidean cost function, a minimiser for the optimal transport problem with general cost is an almost-minimiser for the one with quadratic cost. This allows us to reprove the C^{1,\alpha}-regularity result of De Philippis—Figalli, bypassing Caffarelli’s celebrated theory. (This is joint work with F. Otto and M. Prod’homme)
2022-03-15
16:00hrs.
16:00hrs.
Goncalo Oliveira. Ist Austria
Special Lagrangians and Lagrangian mean curvature flow
Zoom https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
Abstract:
(joint work with Jason Lotay) Richard Thomas and Shing-Tung-Yau proposed two conjectures on the existence of special Lagrangian submanifolds and on the use of Lagrangian mean curvature flow to find them. In this talk, I will report on joint work with Jason Lotay to prove these on certain symmetric hyperKahler 4-manifolds. If time permits I may also comment on our work in progress to tackle more refined conjectures of Dominic Joyce regarding the existence of Bridgeland stability conditions on Fukaya categories and their interplay with Lagrangian mean curvature flow.
Special Lagrangians and Lagrangian mean curvature flow
Zoom https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
Abstract:
(joint work with Jason Lotay) Richard Thomas and Shing-Tung-Yau proposed two conjectures on the existence of special Lagrangian submanifolds and on the use of Lagrangian mean curvature flow to find them. In this talk, I will report on joint work with Jason Lotay to prove these on certain symmetric hyperKahler 4-manifolds. If time permits I may also comment on our work in progress to tackle more refined conjectures of Dominic Joyce regarding the existence of Bridgeland stability conditions on Fukaya categories and their interplay with Lagrangian mean curvature flow.
2022-01-11
16:00hrs.
16:00hrs.
Renato Velozo. University of Cambridge
Stability of Schwarzschild for the spherically symmetric Einstein--massless Vlasov system
Auditorio San Agustín
Abstract:
The Einstein--massless Vlasov system is a relevant model in the study of collisionless many particle systems in general relativity. In this talk, I will present a stability result for the exterior of Schwarzschild as a solution of this system assuming spherical symmetry. We exploit the hyperbolicity of the geodesic flow around the black hole to obtain decay of the energy momentum tensor, despite the presence of trapped null geodesics. The main result requires a precise understanding of radial derivatives of the energy momentum tensor, which we estimate using Jacobi fields on the tangent bundle in terms of the Sasaki metric.
https://reuna.zoom.us/j/83270085704
Stability of Schwarzschild for the spherically symmetric Einstein--massless Vlasov system
Auditorio San Agustín
Abstract:
The Einstein--massless Vlasov system is a relevant model in the study of collisionless many particle systems in general relativity. In this talk, I will present a stability result for the exterior of Schwarzschild as a solution of this system assuming spherical symmetry. We exploit the hyperbolicity of the geodesic flow around the black hole to obtain decay of the energy momentum tensor, despite the presence of trapped null geodesics. The main result requires a precise understanding of radial derivatives of the energy momentum tensor, which we estimate using Jacobi fields on the tangent bundle in terms of the Sasaki metric.
https://reuna.zoom.us/j/83270085704
2022-01-04
16:00hrs.
16:00hrs.
Judith Campos. Universidad Autónoma de México
Desigualdades de Gårding y su impacto en la regularidad y unicidad de funciones minimizantes
https://reuna.zoom.us/j/83185620541
Abstract:
En el contexto de funcionales definidos sobre un espacio de Sobolev del tipo "W^{1,p}_g(\Omega,\mathbb{R}^N)")
, con 
, la cuasiconvexidad del integrando es, a grandes rasgos, equivalente a la semi-continuidad inferior del funcional que éste define. Bajo esta hipótesis, y suponiendo que el integrando crece polinomialmente, L.C. Evans (1986) demostró que las funciones minimizando estos funcionales son de clase 
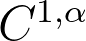fuera de un subconjunto de 
de medida cero. Por otra parte, E. Spadaro (2009) demostró que no podemos esperar tener unicidad de funciones minimizantes de funcionales (fuertemente) cuasiconvexos. En esta plática mostraremos que, si las condiciones de frontera son suficientemente pequeñas, es posible obtener regularidad en el sentido clásico en el conjunto 
y, más aún, que existe una única función minimizante para esta clase de funcionales. Este proyecto ha sido realizado en colaboración con Jan Kristensen.
Desigualdades de Gårding y su impacto en la regularidad y unicidad de funciones minimizantes
https://reuna.zoom.us/j/83185620541
Abstract:
En el contexto de funcionales definidos sobre un espacio de Sobolev del tipo
, con , la cuasiconvexidad del integrando es, a grandes rasgos, equivalente a la semi-continuidad inferior del funcional que éste define. Bajo esta hipótesis, y suponiendo que el integrando crece polinomialmente, L.C. Evans (1986) demostró que las funciones minimizando estos funcionales son de clase fuera de un subconjunto de de medida cero. Por otra parte, E. Spadaro (2009) demostró que no podemos esperar tener unicidad de funciones minimizantes de funcionales (fuertemente) cuasiconvexos. En esta plática mostraremos que, si las condiciones de frontera son suficientemente pequeñas, es posible obtener regularidad en el sentido clásico en el conjunto y, más aún, que existe una única función minimizante para esta clase de funcionales. Este proyecto ha sido realizado en colaboración con Jan Kristensen.
2021-12-07
16:00hrs.
16:00hrs.
Mario Bravo. Universidad Adolfo Ibañez
Universal bounds of fixed point iterations via optimal transport metrics
https://reuna.zoom.us/j/83987391608
Abstract:
In this talk, we study a particular family of metrics over the set of non-negative integers. We show that they provide tight error estimates for a general version of the Krasnosel’skii-Mann
Joint work with Thierry Champion and Roberto Cominetti.
Universal bounds of fixed point iterations via optimal transport metrics
https://reuna.zoom.us/j/83987391608
Abstract:
In this talk, we study a particular family of metrics over the set of non-negative integers. We show that they provide tight error estimates for a general version of the Krasnosel’skii-Mann
iteration for non-expansive maps. We also describe how this approach yields a greedy algorithm for computing them efficiently.
Joint work with Thierry Champion and Roberto Cominetti.
2021-11-23
16:00hrs.
16:00hrs.
Oscar Lasso Andino. Universidad de Las Americas, Quito, Ecuador
The renormalization group flow of the non-linear sigma model in string theory
Zoom https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
Abstract:
The renormalization group flow of the non-linear sigma model in string theory
Zoom https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
Abstract:
In this talk we present an introduction to the renormalization group in string theory.
We start by introducing the worldsheet renormalization group flow equations of the non-linear sigma models. We will discuss about the beta functions and their properties.
We start by introducing the worldsheet renormalization group flow equations of the non-linear sigma models. We will discuss about the beta functions and their properties.
We review some monotonicity results by discussing about Perelman entropies and its geometric interpretation for the Ricci flow approximation. Finally, we present some results about the Perelman entropies for the whole model and its higher order corrections. Finally, we discuss about some applications in the high energy physics and some open problems for the mathematical physics community.
2021-11-16
16:00hrs.
16:00hrs.
Arianna Giunti. Imperial College
Homogenization in randomly perforated domains
Zoom https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
Homogenization in randomly perforated domains
Zoom https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
2021-11-09
16:00hrs.
16:00hrs.
Andrés Zúñiga. Universidad de O'higgins
A nonlocal isoperimetric problem: density perimeter.
https://reuna.zoom.us/j/87136010351
Abstract:
We will discuss a variant of a classical geometric minimization problem, known as the “nonlocal isoperimetric problem”, which arises from studies in Nuclear Physics by Gamow in the 1930’s. By introducing a density in the perimeter functional, we obtain features that differ substantially from existing results in the framework of the classical problem without densities. In the regime of “small” non-local contribution, we completely characterize the minimizer, in the case the density is a monomial radial weight. This work is a collaboration with Stan Alama and Lia Bronsard (McMaster University) and Ihsan Topaloglu (Virginia Commonwealth University), as part of the project QUALITATIVE PROPERTIES OF WEIGHTED AND ANISOTROPIC VARIATIONAL PROBLEMS financed by ANID CHILE FONDECYT INICIACION Nº 11201259.
A nonlocal isoperimetric problem: density perimeter.
https://reuna.zoom.us/j/87136010351
Abstract:
We will discuss a variant of a classical geometric minimization problem, known as the “nonlocal isoperimetric problem”, which arises from studies in Nuclear Physics by Gamow in the 1930’s. By introducing a density in the perimeter functional, we obtain features that differ substantially from existing results in the framework of the classical problem without densities. In the regime of “small” non-local contribution, we completely characterize the minimizer, in the case the density is a monomial radial weight. This work is a collaboration with Stan Alama and Lia Bronsard (McMaster University) and Ihsan Topaloglu (Virginia Commonwealth University), as part of the project QUALITATIVE PROPERTIES OF WEIGHTED AND ANISOTROPIC VARIATIONAL PROBLEMS financed by ANID CHILE FONDECYT INICIACION Nº 11201259.
2021-08-31
16:00hrs.
16:00hrs.
Mauricio Godoy. Universidad de la Frontera
Una Invitación a Las Simetrías Infinitesimales
https://reuna.zoom.us/j/85651430727
https://reuna.zoom.us/j/85651430727
Una Invitación a Las Simetrías Infinitesimales
https://reuna.zoom.us/j/85651430727
https://reuna.zoom.us/j/85651430727
2021-08-17
16:00hrs.
16:00hrs.
Adolfo Vargas-Jiménez. University of Alberta
Unique Monge type solutions in the multi-marginal optimal transport via graph theory
https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
Unique Monge type solutions in the multi-marginal optimal transport via graph theory
https://zoom.us/j/95659148169?pwd=SHNlM0w3TUdkM04xMEJUeDBHWmdJdz09
2021-05-25
14:00hrs.
14:00hrs.
Ujué Etayo. Universidad de Cantabria
Sobre procesos de puntos determinantales
https://zoom.us/j/93411180186
Abstract:
Entre los distintos procesos de puntos aleatorios, los llamados determinantales presentan varias características que los hacen firmes candidatos para resolver problemas de equidistribución: exhiben repulsión local, tienden a distribuirse uniformemente y son fácilmente computables. En esta charla presentaré las principales características de estos procesos, cómo definirlos en distintos tipos de espacios y dos aplicaciones concretas en esferas de dimensión arbitraria.
Sobre procesos de puntos determinantales
https://zoom.us/j/93411180186
Abstract:
Entre los distintos procesos de puntos aleatorios, los llamados determinantales presentan varias características que los hacen firmes candidatos para resolver problemas de equidistribución: exhiben repulsión local, tienden a distribuirse uniformemente y son fácilmente computables. En esta charla presentaré las principales características de estos procesos, cómo definirlos en distintos tipos de espacios y dos aplicaciones concretas en esferas de dimensión arbitraria.
2021-05-04
17:00hrs.
17:00hrs.
Rodolfo Viera. Pontificia Universidad Católica de Chile
Conjuntos de Delone y equivalencia (bi)-Lipschitz
Zoom, https://zoom.us/j/93411180186
Abstract:
Conjuntos de Delone y equivalencia (bi)-Lipschitz
Zoom, https://zoom.us/j/93411180186
Abstract:
Un conjunto de Delone D en un espacio métrico X es un subconjunto uniformemente discreto y relativamente denso.
Una pregunta natural que surge es ver si todo conjunto de Delone en un espacio Euclidiano es (bi)-Lipschitz equivalente a un lattice.
En esta charla intentaremos abordar esta pregunta, de naturaleza puramente discreta, tanto desde un punto de vista anaítico como geométrico.
2020-08-25
17:10hrs.
17:10hrs.
Nicolás Vilches. Pontificia Universidad Católica de Chile
Invertibilidad global en espacios de Sobolev: parte II
Zoom, ID de reunión: 914 0230 0356 Código de acceso: Laplace
Abstract:
Invertibilidad global en espacios de Sobolev: parte II
Zoom, ID de reunión: 914 0230 0356 Código de acceso: Laplace
Abstract:
En esta charla nos enfocaremos en una de las herramientas mencionadas durante la parte I, respecto a cómo recuperar el determinante de la matriz jacobiana de manera distribucional. Estudiaremos una conjetura propuesta por John Ball en 1976, junto con un ejemplo que ilustra la posibilidad de tener un determinante distribucional distinto al puntual. Posteriormente, seguiremos la demostración de Stefan Müller a la conjetura (en 1990), a partir de un resultado más general. La herramienta principal será una versión refinada del teorema de diferenciación de Lebesgue, debida a Alberto Calderón y Antoni Zygmund.
2020-08-18
17:10hrs.
17:10hrs.
Duvan Henao. Pontificia Universidad Católica de Chile
Invertibilidad global en espacios de Sobolev: parte I
Zoom Meeting ID: 980 2662 5924 Passcode: Brouwer
Abstract:
La charla trata sobre la regularidad requerida para definir el grado topológico en espacios de Sobolev, a modo de mantener una de sus propiedades esenciales: si el grado de una función es igual a uno, con respecto a un punto y del espacio, restringiendo la función a una subregión E del dominio, entonces el punto y tiene exactamente una preimagen en la subregión E. Esto se usa en elasticidad para garantizar que no haya interpenetración de la materia (al menos para el problema Dirichlet donde el desplazamiento se prescribe en toda la frontera). Junto a Carlos Mora Corral y a Marcos de la Oliva hemos relajado las condiciones de regularidad para que se mantenga esa propiedad del grado. El análisis está conectado con la estructura analítica de los menores de un gradiente (en particular la identidad de Piola) y la rigidez geométrica. Las ideas presentadas podrían ayudar a establecer que ciertas funciones son difeomorfismos, incluso en contextos con variedades diferenciales de dimensión muy grande.
https://zoom.us/j/98026625924?pwd=WE5yaXRjNDc1S2xMQXFsdThBaXhrQT09
Invertibilidad global en espacios de Sobolev: parte I
Zoom Meeting ID: 980 2662 5924 Passcode: Brouwer
Abstract:
La charla trata sobre la regularidad requerida para definir el grado topológico en espacios de Sobolev, a modo de mantener una de sus propiedades esenciales: si el grado de una función es igual a uno, con respecto a un punto y del espacio, restringiendo la función a una subregión E del dominio, entonces el punto y tiene exactamente una preimagen en la subregión E. Esto se usa en elasticidad para garantizar que no haya interpenetración de la materia (al menos para el problema Dirichlet donde el desplazamiento se prescribe en toda la frontera). Junto a Carlos Mora Corral y a Marcos de la Oliva hemos relajado las condiciones de regularidad para que se mantenga esa propiedad del grado. El análisis está conectado con la estructura analítica de los menores de un gradiente (en particular la identidad de Piola) y la rigidez geométrica. Las ideas presentadas podrían ayudar a establecer que ciertas funciones son difeomorfismos, incluso en contextos con variedades diferenciales de dimensión muy grande.
https://zoom.us/j/98026625924?pwd=WE5yaXRjNDc1S2xMQXFsdThBaXhrQT09
2020-01-21
16:00hrshrs.
16:00hrshrs.
Barbara Brandolini. Departamento de Matemáticas, Universidad de Nápoles, Italia
Improved bounds for Hermite-Hadamard inequalities in higher dimensions
Sala 2, Facultad de Matemáticas
Abstract:
ver pdf
Improved bounds for Hermite-Hadamard inequalities in higher dimensions
Sala 2, Facultad de Matemáticas
Abstract:
ver pdf
2019-12-03
16:00hrs.
16:00hrs.
Rafael Benguria. P. Universidad Católica de Chile
A General Brezis-Nirenberg Problem
Facultad de Matemáticas, sala 2
Abstract:
In this talk I will discuss existence, nonexistence and uniqueness of solutions for a general Brezis-Nirenberg problem. The region of parameters for which there is existence and nonexistence of positive solutions is characterized by two spectral problems that have interest on their own. This is joint
A General Brezis-Nirenberg Problem
Facultad de Matemáticas, sala 2
Abstract:
In this talk I will discuss existence, nonexistence and uniqueness of solutions for a general Brezis-Nirenberg problem. The region of parameters for which there is existence and nonexistence of positive solutions is characterized by two spectral problems that have interest on their own. This is joint
work with Soledad Benguria (U. Wisconsin, Madison).
2019-11-05
16:30hrs.
16:30hrs.
Francois Murat. Laboratoire Jacques-Louis Lions Sorbonne Université & Cnrs
Definition, existence, stability and uniqueness of the solution to a semilinear elliptic problem with a singularity at u = 0
Facultad de Matematicas, sala 2
Definition, existence, stability and uniqueness of the solution to a semilinear elliptic problem with a singularity at u = 0
Facultad de Matematicas, sala 2
Contáctenos
Edificio Rolando Chuaqui, Campus San Joaquín. Avda. Vicuña Mackenna 4860, Macul, Chile.Teléfono (+56) 95504 4511.
Formulario de Contacto